降维算法

概述

sklearn 中的降维算法

sklearn 中降维算法都被包括在模块 decomposition 中，这个模块本质是一个矩阵分解模块。

• 主成分分析
  • 主成分分析（PCA）：PCA
  • 增量主成分分析（IPCA）：IncrementalPCA
  • 核主成分分析（KPCA）：KernelPCA
  • 小批量稀疏主成分分析：MiniBatchSparsePCA
  • 稀疏主成分分析：SparsePCA
  • 截断的SVD（LSA）：TruncatedSVD
• 因子分析
  • 因子分析（FA）：FactorAnalysis
• 独立成分分析
  • 独立成分分析的快速算法：FastICA
• 字典学习
  • 字典学习：DictionaryLearning
  • 小批量字典学习：MiniBatchDictionaryLearning
  • 字典学习用于矩阵分解：dict_learning
  • 在线字典学习用于矩阵分解：dict_learning_online
• 高级矩阵分解
  • 具有在线变分贝叶斯算法的隐含狄利克雷分布：LatentDirichletAllocation
  • 非负矩阵分解（NMF）：NMF
• 其他矩阵分解
  • 稀疏编码：SparseCoder

PCA 和 SVD 都属于矩阵分解算法中的入门算法，都是通过分解特征矩阵来进行降维，它们也是我们今天要讲解的重点。

PCA 与 SVD

在降维的过程中，能够既减少特征的数量，又保留大部分有效信息——删除那些无效信息的特征，将那些带有重复信息的特征合并——逐渐创造出能够代表原特征矩阵大部分信息的、特征更少的新特征矩阵。

PCA 中使用的信息量衡量指标，就是样本方差，又称为可解释方差，方差越大，特征所带的信息量越多。

\[Var = \frac{1}{n-1}\sum_{i=1}^{n}(x_i-\hat{a})\]

降维究竟是怎样实现的？

以一组简单的二维数据为例，讲解降维原理。

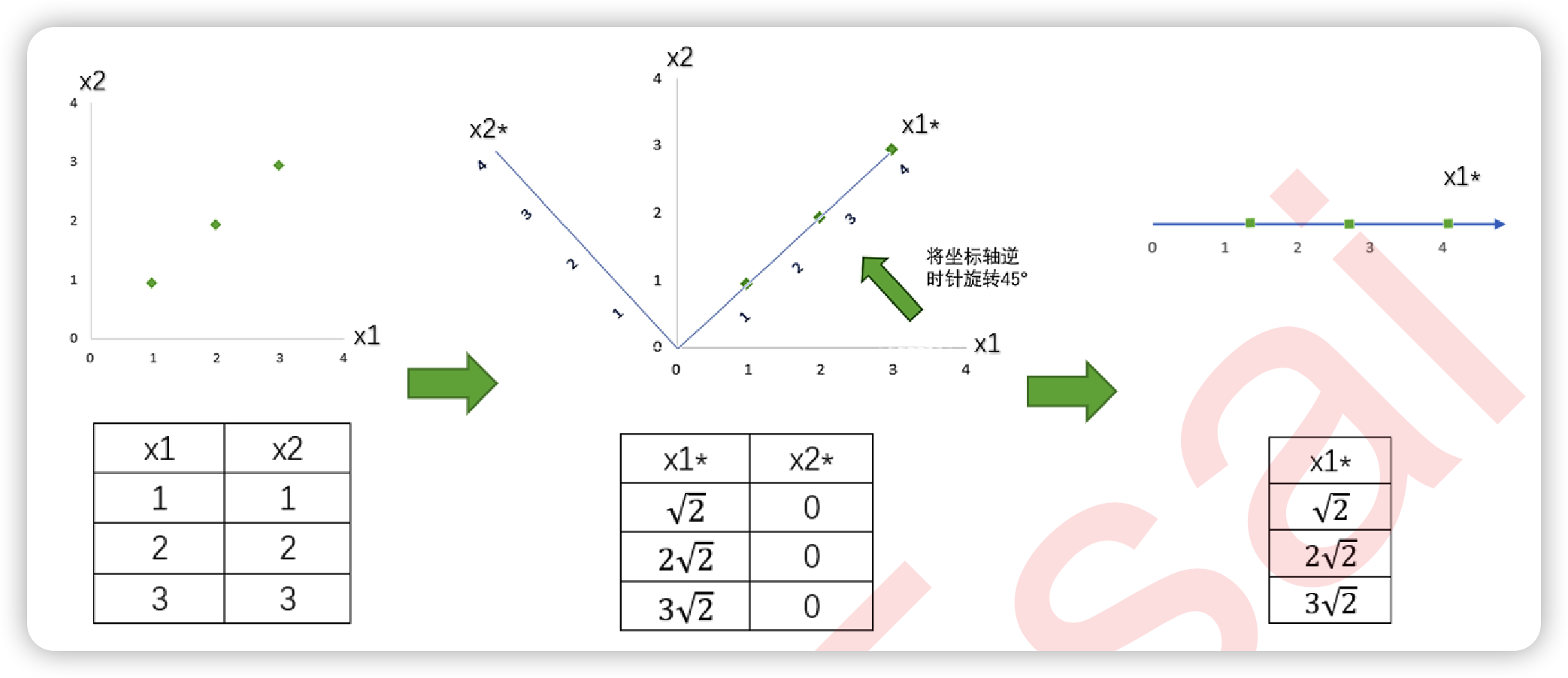
原始的方差：

\[var(x_1) = var(x_2) = \frac{1}{2}((1-2)^2+(2-2)^2+(3-2)^2) = 1\]

坐标旋转后的方差：

\[\begin{align} var(x_1^*) &= \frac{1}{2}((\sqrt{2}-2\sqrt{2})^2+(2\sqrt{2}-2\sqrt{2})^2+(3\sqrt{2}-2\sqrt{2})^2) = 2 \\ var(x_2^*) &= 0 \end{align}\]

随后，删除特征 x2*，原来的二维数据降为一维数据，成功实现降维。在这个特殊的例子中，坐标变化前后的总方差不变，说明降维后信息量没有减少，即完整保留了原始数据的信息。

降维算法可以理解为：对于位于原始 n 维空间 V 的原数据 (m,n)，找出新的 n 维空间 V’ 及对应的空间变换后的数据 (m’,n’)，让数据被压缩到 k（k小于n）维空间后，总信息量损失尽可能少。

PCA 和 SVD 是两种不同的降维算法，都遵从上述原理来实现降维，只是两种算法中矩阵分解的方法不同。

\[X' \xrightarrow{\text{去中心化}} X \xrightarrow{\text{协方差矩阵}} \frac{1}{n-1}XX^T \xrightarrow{\text{特征分解}} Q \Sigma Q^{-1}\]

class sklearn.decomposition.PCA(n_components=None, *, copy=True, whiten=False, svd_solver=’auto’, tol=0.0, iterated_power=’auto’, random_state=None)å